안녕하세요. 개발자 움탱입니다.
이 게시물은 알고리즘을 배우면서 학습한 내용을 문서화하기 위한 것입니다.
그래서 저는 각 설명을 편안하게 저널링하고 짧은 형식으로 기록하려고 노력합니다.
더 좋은 방법이 있거나 잘 이해되지 않는 부분이 있으면 알려주시면 감사하겠습니다.
좋은 하루 되세요:)
https://www.acmicpc.net/problem/2491
2491호: 시리얼
0에서 9까지 N개의 숫자 시퀀스가 있습니다. 해당 시퀀스에서 연속 증가(동일 포함) 또는 연속 감소(동일 포함) 시퀀스의 가장 긴 시퀀스를 찾습니다.
www.acmicpc.net
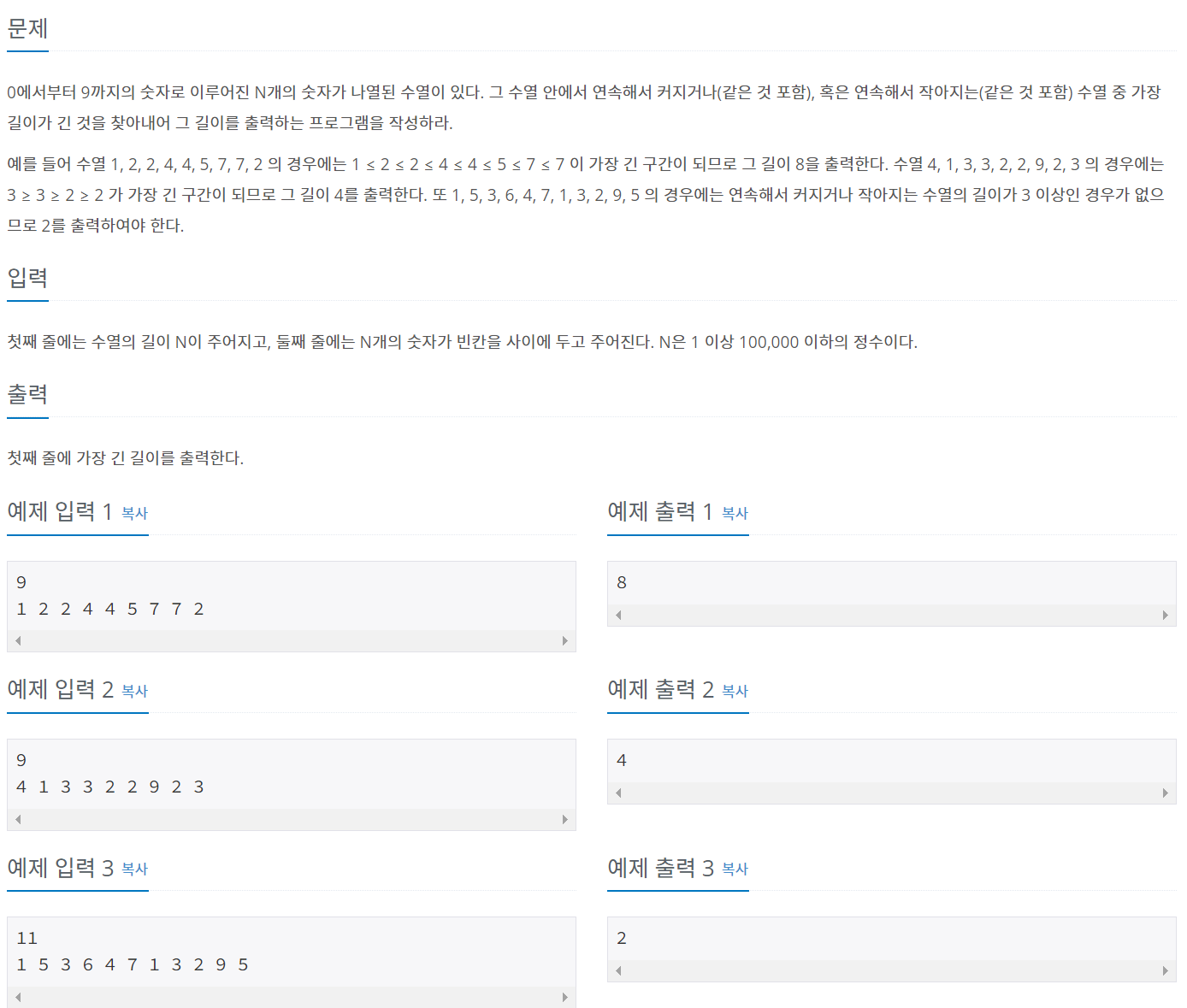
문제 설명
문제를 잘 읽으시면 저절로 이해가 되실 테니 위의 문제들을 천천히 읽어보시길 권합니다.
논평
위의 질문 계속 성장 연속적으로 감소하는 일련의 숫자를 찾는 문제따라서 이중 확인이 필요합니다.
- 처음부터 번호 처음부터 끝까지 상승 길이를 찾기 위해 탐색긴 길이를 찾아라
- 1의 반대 마지막 번호부터 처음부터 첫 번째 숫자까지 상승 길이를 찾기 위해 탐색긴 길이를 찾아라
1번은 이해가 되는데 2번은 이해가 안되네요.
왜? 내림차순에서 더 긴 수열을 찾고 오름차순 수열(증가 수열)의 길이를 찾는 이유는 무엇입니까?
이유는 간단하다 수열의 내림차순은 역수열의 오름차순이므로 마지막 숫자부터 수열을 찾아 오름차순의 길이를 구한다.예.
dp 방식으로 기록한 위의 방식을 이해하면 가장 긴 길이를 찾는다.
코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String() args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
StringTokenizer st = new StringTokenizer(br.readLine());
int() arr = new int(N);
for (int i = 0; i < N; i++) {
arr(i) = Integer.parseInt(st.nextToken());
}
int maxCount = 1;
int prev = arr(0);
int count = 1;
// 처음을 시작으로 오름차순 길이 찾기
for (int i = 1; i < N; i++) {
if (prev <= arr(i)) {
count++;
maxCount = Math.max(maxCount, count);
} else {
count = 1;
}
prev = arr(i);
}
prev = arr(N - 1);
count = 1;
// 마지막을 시작으로 오름차순 길이 찾기
for (int i = N - 2; i >= 0; i--) {
if (prev <= arr(i)) {
count++;
maxCount = Math.max(maxCount, count);
} else {
count = 1;
}
prev = arr(i);
}
System.out.println(maxCount);
br.close();
}
}